Tools and Techniques in Artificial Intelligence

Search and optimization

Many problems in AI can be solved theoretically by intelligently searching through many possible solutions: Reasoning can be reduced to performing a search. For example, logical proof can be viewed as searching for a path that leads from premises to conclusions, where each step is the application of an inference rule. Planning algorithms search through trees of goals and subgoals, attempting to find a path to a target goal, a process called means-ends analysis. Robotics algorithms for moving limbs and grasping objects use local searches in configuration space.

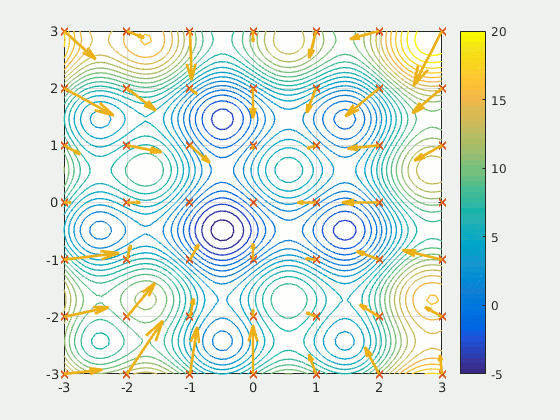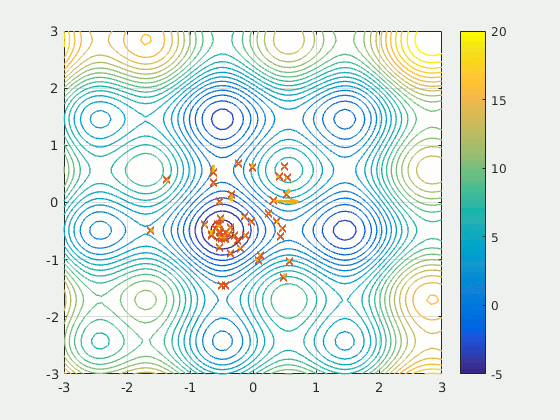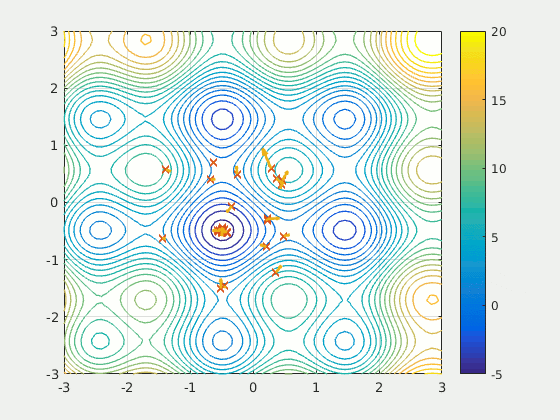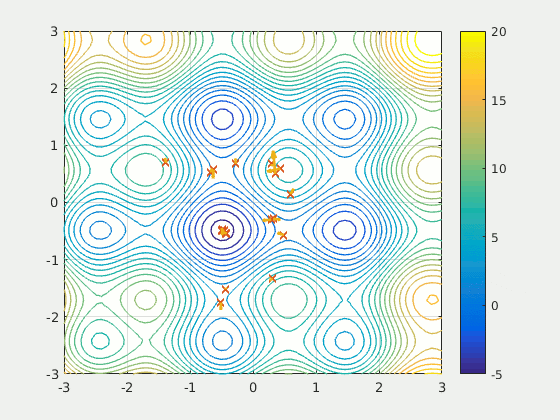Simple exhaustive searches are rarely sufficient for most real-world problems: the search space (the number of places to search) quickly grows to astronomical numbers. The result is a search that is too slow or never completes. The solution, for many problems, is to use "heuristics" or "rules of thumb" that prioritize choices in favor of those more likely to reach a goal and to do so in a shorter number of steps. In some search methodologies heuristics can also serve to eliminate some choices unlikely to lead to a goal (called "pruning the search tree"). Heuristics supply the program with a "best guess" for the path on which the solution lies. Heuristics limit the search for solutions into a smaller sample size.

A particle swarm seeking the global minimum A very different kind of search came to prominence in the 1990s, based on the mathematical theory of optimization. For many problems, it is possible to begin the search with some form of a guess and then refine the guess incrementally until no more refinements can be made. These algorithms can be visualized as blind hill climbing: we begin the search at a random point on the landscape, and then, by jumps or steps, we keep moving our guess uphill, until we reach the top. Other optimization algorithms are simulated annealing, beam search and random optimization. Evolutionary computation uses a form of optimization search. For example, they may begin with a population of organisms (the guesses) and then allow them to mutate and recombine, selecting only the fittest to survive each generation (refining the guesses). Classic evolutionary algorithms include genetic algorithms, gene expression programming, and genetic programming. Alternatively, distributed search processes can coordinate via swarm intelligence algorithms. Two popular swarm algorithms used in search are particle swarm optimization (inspired by bird flocking) and ant colony optimization (inspired by ant trails).

Logic

Logic is used for knowledge representation and problem solving, but it can be applied to other problems as well. For example, the satplan algorithm uses logic for planning and inductive logic programming is a method for learning.

Several different forms of logic are used in AI research. Propositional logic involves truth functions such as "or" and "not". First-order logic adds quantifiers and predicates, and can express facts about objects, their properties, and their relations with each other. Fuzzy logic assigns a "degree of truth" (between 0 and 1) to vague statements such as "Alice is old" (or rich, or tall, or hungry), that are too linguistically imprecise to be completely true or false. Default logics, non-monotonic logics and circumscription are forms of logic designed to help with default reasoning and the qualification problem. Several extensions of logic have been designed to handle specific domains of knowledge, such as: description logics; situation calculus, event calculus and fluent calculus (for representing events and time); causal calculus; belief calculus (belief revision); and modal logics. Logics to model contradictory or inconsistent statements arising in multi-agent systems have also been designed, such as paraconsistent logics.

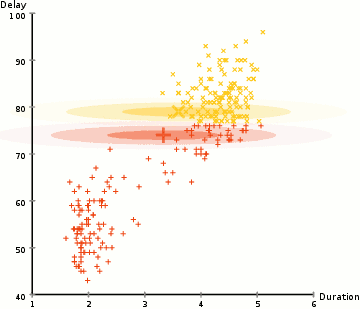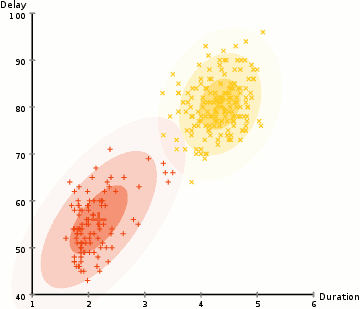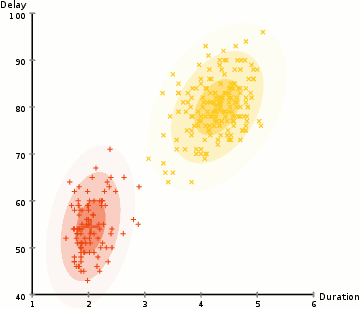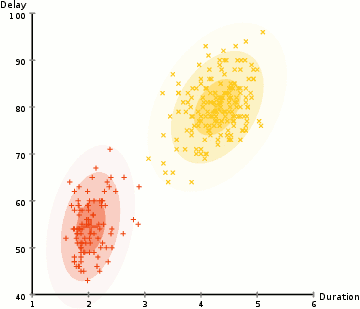
Probabilistic methods for uncertain reasoning

Many problems in AI (in reasoning, planning, learning, perception, and robotics) require the agent to operate with incomplete or uncertain information. AI researchers have devised a number of powerful tools to solve these problems using methods from probability theory and economics. Bayesian networks are a very general tool that can be used for various problems: reasoning (using the Bayesian inference algorithm),[n] learning (using the expectation-maximization algorithm),[o] planning (using decision networks) and perception (using dynamic Bayesian networks). Probabilistic algorithms can also be used for filtering, prediction, smoothing and finding explanations for streams of data, helping perception systems to analyze processes that occur over time (e.g., hidden Markov models or Kalman filters).

A key concept from the science of economics is "utility": a measure of how valuable something is to an intelligent agent. Precise mathematical tools have been developed that analyze how an agent can make choices and plan, using decision theory, decision analysis, and information value theory. These tools include models such as Markov decision processes, dynamic decision networks, game theory and mechanism design.

Classifiers and statistical learning methods

The simplest AI applications can be divided into two types: classifiers ("if shiny then diamond") and controllers ("if diamond then pick up"). Controllers do, however, also classify conditions before inferring actions, and therefore classification forms a central part of many AI systems. Classifiers are functions that use pattern matching to determine a closest match. They can be tuned according to examples, making them very attractive for use in AI. These examples are known as observations or patterns. In supervised learning, each pattern belongs to a certain predefined class. A class is a decision that has to be made. All the observations combined with their class labels are known as a data set. When a new observation is received, that observation is classified based on previous experience.

A classifier can be trained in various ways; there are many statistical and machine learning approaches. The decision tree is the simplest and most widely used symbolic machine learning algorithm. K-nearest neighbor algorithm was the most widely used analogical AI until the mid-1990s. Kernel methods such as the support vector machine (SVM) displaced k-nearest neighbor in the 1990s. The naive Bayes classifier is reportedly the "most widely used learner" at Google, due in part to its scalability. Neural networks are also used for classification.

Classifier performance depends greatly on the characteristics of the data to be classified, such as the dataset size, distribution of samples across classes, the dimensionality, and the level of noise. Model-based classifiers perform well if the assumed model is an extremely good fit for the actual data. Otherwise, if no matching model is available, and if accuracy (rather than speed or scalability) is the sole concern, conventional wisdom is that discriminative classifiers (especially SVM) tend to be more accurate than model-based classifiers such as "naive Bayes" on most practical data sets.

#Artificial neural networks Neural networks were inspired by the architecture of neurons in the human brain. A simple "neuron" N accepts input from other neurons, each of which, when activated (or "fired"), casts a weighted "vote" for or against whether neuron N should itself activate. Learning requires an algorithm to adjust these weights based on the training data; one simple algorithm (dubbed "fire together, wire together") is to increase the weight between two connected neurons when the activation of one triggers the successful activation of another. Neurons have a continuous spectrum of activation; in addition, neurons can process inputs in a nonlinear way rather than weighing straightforward votes.

Modern neural networks model complex relationships between inputs and outputs or and find patterns in data. They can learn continuous functions and even digital logical operations. Neural networks can be viewed a type of mathematical optimization — they perform a gradient descent on a multi-dimensional topology that was created by training the network. The most common training technique is the backpropagation algorithm. Other learning techniques for neural networks are Hebbian learning ("fire together, wire together"), GMDH or competitive learning.

The main categories of networks are acyclic or feedforward neural networks (where the signal passes in only one direction) and recurrent neural networks (which allow feedback and short-term memories of previous input events). Among the most popular feedforward networks are perceptrons, multi-layer perceptrons and radial basis networks.

Deep learning

Deep learning uses several layers of neurons between the network's inputs and outputs. The multiple layers can progressively extract higher-level features from the raw input. For example, in image processing, lower layers may identify edges, while higher layers may identify the concepts relevant to a human such as digits or letters or faces. Deep learning has drastically improved the performance of programs in many important subfields of artificial intelligence, including computer vision, speech recognition, image classification and others.

Deep learning often uses convolutional neural networks for many or all of its layers. In a convolutional layer, each neuron receives input from only a restricted area of the previous layer called the neuron's receptive field. This can substantially reduce the number of weighted connections between neurons, and creates a hierarchy similar to the organization of the animal visual cortex.

In a recurrent neural network the signal will propagate through a layer more than once; thus, an RNN is an example of deep learning. RNNs can be trained by gradient descent, however long-term gradients which are back-propagated can "vanish" (that is, they can tend to zero) or "explode" (that is, they can tend to infinity), known as the vanishing gradient problem. The long short term memory (LSTM) technique can prevent this in most cases.